How to Fix Quantum Computing Bugs

It is a law of physics that everything that is not prohibited is mandatory. Errors are thus unavoidable. They are everywhere: in language, cooking, communication, image processing and, of course, computation. Mitigating and correcting them keeps society running. You can scratch a DVD yet still play it. QR codes can be blurred or torn yet are still readable. Images from space probes can travel hundreds of millions of miles yet still look crisp. Error correction is one of the most fundamental concepts in information technology. Errors may be inevitable, but they are also fixable.
This law of inevitability applies equally to quantum computers. These emerging machines exploit the fundamental rules of physics to solve problems that classical computers find intractable. The implications for science and business could be profound. But with great power comes great vulnerability. Quantum computers suffer types of errors that are unknown to classical computers and that our standard correction techniques cannot fix.
I am a physicist working in quantum computing at IBM, but my career didn’t start there. I began as a condensed-matter theorist investigating materials’ quantum-mechanical behavior, such as superconductivity; at the time I was oblivious to how that would eventually lead me to quantum computation. That came later when I took a hiatus to work on science policy at the U.S. Department of State, which next led me to the Defense Advanced Research Projects Agency (DARPA) and the Intelligence Advanced Research Projects Activity (IARPA). There I sought to employ the fundamentals of nature to develop new technology.
Quantum computers were in their earliest stages then. Although Paul Benioff of Argonne National Laboratories had proposed them in 1980, it took physicists nearly two decades to build the first one. Another decade later, in 2007, they invented the basic data unit that underlies the quantum computers of IBM, Google and others, known as the superconducting transmon qubit. My experience with superconductivity was suddenly in demand. I helped run several quantum-computing research programs at IARPA and later joined IBM.
There I devoted myself to improving operations among multiple linked qubits and exploring how to correct errors. By combining qubits through a quantum phenomenon called entanglement, we can store vast amounts of information collectively, much more than the same number of ordinary computer bits can. Because qubit states are in the form of waves, they can interfere, just as light waves do, leading to a much richer landscape for computation than just flipping bits. These capabilities give quantum computers their power to perform certain functions extremely efficiently and potentially speed up a wide range of applications: simulating nature, investigating and engineering new materials, uncovering hidden features in data to improve machine learning, or finding more energy-efficient catalysts for industrial chemical processes.
The trouble is that many proposals to solve useful problems require quantum computers to perform billions of logical operations, or “gates,” on hundreds to thousands of qubits. That feat demands they make at most a single error every billion gates. Yet today’s best machines make an error every 1,000 gates. Faced with the huge gap between theory and practice, physicists in the early days worried that quantum computing would remain a scientific curiosity.
Correcting errors
The game changed in 1995, when Peter Shor of Bell Labs and, independently, Andrew Steane of the University of Oxford developed quantum error correction. They showed how physicists can spread a single qubit’s worth of information over multiple physical qubits, to build reliable quantum computers out of unreliable components. So long as the physical qubits are of high-enough quality that their error rate is below some threshold, we can remove errors faster than they accumulate.
To see why Shor’s and Steane’s work was such a breakthrough, consider how ordinary error correction typically works. A simple error correction code makes backup copies of information—for example, representing 0 by 000 and 1 by 111. That way, if your computer reads out a 010, it knows the original value was probably 0. Such a code succeeds when the error rate is low enough that at most one copy of the bit is corrupted. Engineers make the hardware as reliable as they can, then add a layer of redundancy to clean up any remaining errors.

It was not clear, however, how to adapt classical methods of error correction to quantum computers. Quantum information cannot be copied; to correct errors, we need to collect information about them through measurement. The problem is, if you check the qubits, you can collapse their state—that is, you can destroy the quantum information encoded in them. Furthermore, besides having errors in flipped bits, in a quantum computer you also have errors in the phases of the waves describing the states of the qubits.
To get around all these issues, quantum error correction strategies use helper qubits. A series of gates entangles the helpers with the original qubits, which effectively transfers noise from the system to the helpers. You then measure the helpers, which gives you enough information to identify the errors without touching the system you care about, therefore letting you fix them.

As with classical error correction, success depends on the physics of the noise. For quantum computers, errors arise when the device gets entangled with the environment. To keep a computer working, the physical error rate must be small enough. There is a critical value for this error rate. Below this threshold you can correct errors to make the probability that a computation will fail arbitrarily low. Above this point, the hardware introduces errors faster than we can correct them. This shift in behavior is essentially a phase transition between an ordered and a disordered state. This fascinated me as a theoretical condensed-matter physicist who spent most of her career studying quantum phase transitions.
We are continuing to investigate ways to improve error correction codes so that they can handle higher error rates, a wider variety of errors, and the constraints of hardware. The most popular error correction codes are called topological quantum codes. Their origins go back to 1982, when Frank Wilczek of the Massachusetts Institute of Technology proposed that the universe might contain an entirely new category of particles. Unlike the known types, which have either integer or half-odd-integer values of angular momentum, the new breed could have fractional values in between. He called them “anyons” and cautioned that “practical applications of these phenomena seem remote.”
But soon physicists discovered that anyons were not so esoteric after all; in fact they have connections to real-world phenomena. To complete their migration from theory to the practical needs of technology, Alexei Kitaev of the California Institute of Technology realized that anyons are a useful formulation for quantum computation. He further proposed using certain systems of many particles as quantum error correction codes.
In these systems, the particles are connected in a lattice structure where their lowest energy state is highly entangled. The errors correspond to the system being in a higher energy state, called an excitation. These excitations are anyons. This system marks the birth of topological codes—and with it, another connection between condensed matter physics and quantum error correction. Because noise is expected to act locally on the lattice, and topological codes have localized excitations, they quickly became the favorite scheme to protect quantum information.
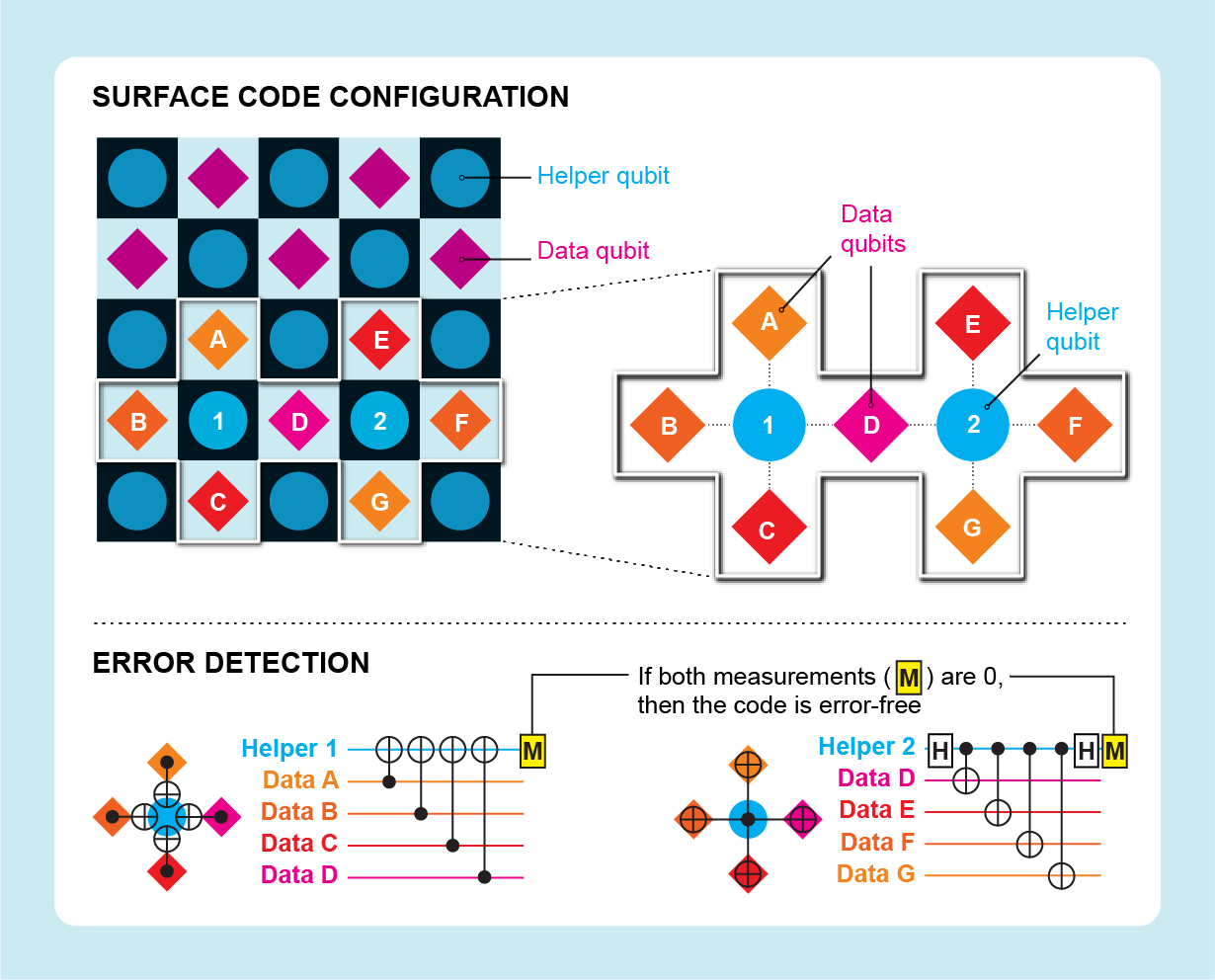
Two examples of topological codes are called the surface code and the color code. The surface code was created by Kitaev and my IBM colleague Sergey Bravyi. It features data and helper qubits alternating on a two-dimensional square grid like black and white squares on a chessboard.
From Chessboards to Settlers of Catan
The theory behind surface codes is compelling, but when we started to explore them at IBM, we ran into challenges. Understanding these requires a little more knowledge of how transmon qubits work.
A transmon qubit relies on oscillating currents traveling around an electrical circuit of superconducting wire. The qubit 0 and 1 values correspond to different superpositions of electric charge. To perform operations on the qubit, we apply pulses of microwave energy at a specific frequency. We have some flexibility in what frequency we choose, and we set it when we fabricate the qubit, choosing different frequencies for different qubits to be able to address them individually. The trouble is that the frequency may deviate from the intended value, or pulses may overlap in frequency, so that a pulse meant for one qubit could change the value of a neighbor. The surface code’s dense grid, where each qubit connects with four other qubits, was causing too many of these frequency collisions.
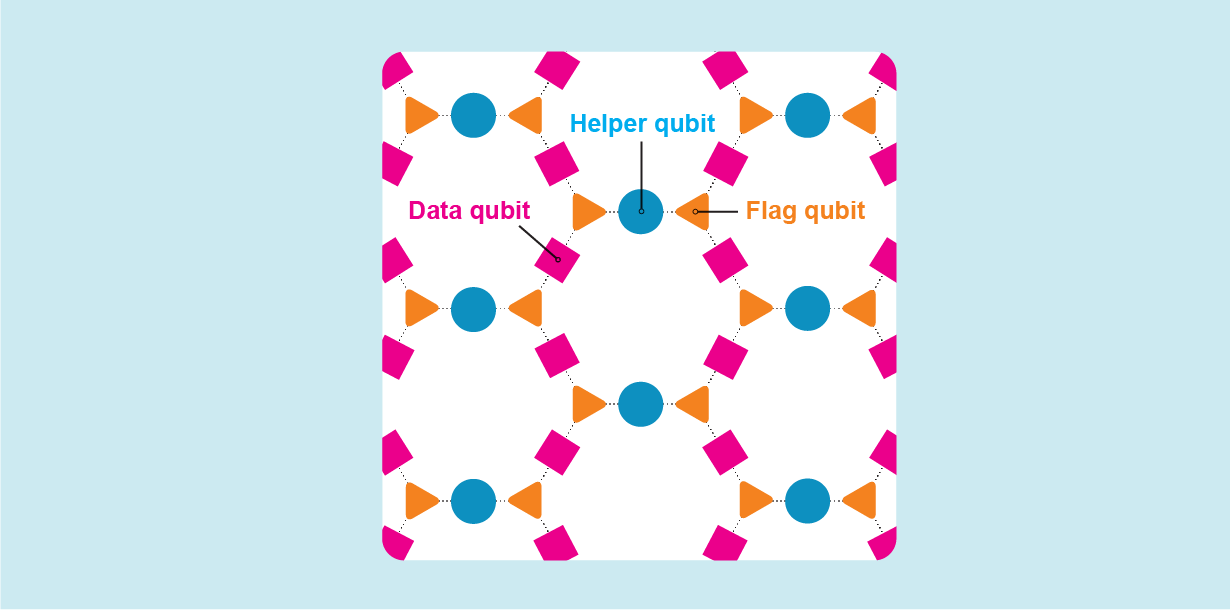
Our team decided to solve the problem by connecting each qubit to fewer neighbors. The resulting lattice consisted of hexagons—we call it the “heavy hex” layout—and looks like the Settlers of Catan game board rather than a chessboard. The good news was that the heavy hex layout reduced the frequency of collisions. But for this layout to be valuable, the IBM theory team had to develop a new error correction code.
The new code, called the heavy hexagon code, combined features of the surface code and of another lattice-based code called the Bacon-Shor code. The lower qubit connectivity in our code means that some qubits, called flag qubits, must serve as intermediaries to identify which errors have occurred, leading to slightly more complex circuits and therefore a slightly lower error threshold for success. But we have found the trade-off is worth it.
There is another problem yet to solve. Codes living on two-dimensional planes and incorporating only nearest-neighbor connections have a large overhead. Correcting more errors means building a larger code, which employs more physical qubits to create a single logical qubit. The setup requires more physical hardware to represent the same amount of data—and more hardware makes it more difficult to build qubits good enough to beat the error threshold.
Quantum engineers have two options. We could make peace with the large overhead—the extra qubits and gates—as the cost of a simpler architecture and work to understand and optimize the different factors contributing to the cost. Alternatively, we could continue to seek better codes. For instance, to encode more logical qubits into fewer physical qubits, perhaps we should allow qubits to interact with more distant qubits than just their nearest neighbors or go beyond a two-dimensional grid to a three- or higher-dimensional lattice. Our theory team is pursuing both options.
The importance of Universality
A useful quantum computer must be able to carry out any possible computational operation. Neglecting this requirement is the root of many common misconceptions and misleading messages about quantum computation. Put simply, not all the devices that people call quantum “computers” are actually computers—many are more like calculating machines that can perform only certain tasks.
Overlooking the need for universal computation is also the root of misconceptions and misleading messages about logical qubits and quantum error correction. Protecting information in memory from error is a start, but it is not enough. We need a universal set of quantum gates, one that is sufficiently rich to perform any gate that is allowed by quantum physics. Then we need to make those gates robust to errors. This is where things get difficult.
Some gates are easy to protect against errors—they fall into a category called transversal gates. To understand these gates, consider two levels of description: the logical qubit (the error-protected unit of information) and the physical qubits (the hardware-level devices that, working together, encode and protect the logical qubit). To perform an error-protected one-qubit transversal gate, you perform the gate on all the physical qubits encoding the logical qubit. To operate an error-protected transversal gate between multiple logical qubits, you operate the gate between corresponding physical qubits in the logical qubits. You can think of the logical qubits as two blocks of physical qubits, called block A and block B. To implement a logical (that is, error-protected) transversal gate, you perform the gate between qubit 1 of block A and qubit 1 of block B, qubit 2 of block A and qubit 2 of block B, and so on for all qubits in the blocks. Because only corresponding qubits are interacting, transversal gates leave the number of errors per block unchanged and therefore under control.
If the entire universal set of quantum gates were transversal, life would be easy. But a fundamental theorem states that no quantum error correction code can perform universal computation using only transversal gates. We can’t have everything in life—or in quantum error correction.
This tells us something important about quantum computers. If you hear anyone say that what is special about quantum computing is that you have superposition and entanglement, beware! Not all superposition and entangled states are special. Some are implemented by a group of transversal gates that we call the Clifford group. A classical computer can efficiently simulate quantum computations using only Clifford gates. What you need are non-Clifford gates, which tend to not be transversal and are difficult to simulate classically.
The best trick we have to implement non-Clifford gates that are protected from noise is called magic state distillation, developed by Kitaev and Bravyi. You can implement non-Clifford gates using only Clifford gates if you have access to a special resource called magic states. Those magic states, however, must be very pure—in other words, have very few errors. Kitaev and Bravyi realized that in some cases, you can start from a collection of noisy magic states and distill them to end up with fewer but purer magic states by using only perfect Clifford gates (here you assume that the Clifford gates are already error-corrected) and measurements to detect and correct errors. Repeating the distillation procedure many times gives you a pure magic state out of the many noisy ones.
Once you have the pure magic state, you can make it interact with the data qubit using a process called teleportation that transfers the data qubit’s state into the new state that the non-Clifford gate would have produced. The magic state is consumed in the process.
Clever though this approach is, it is also extremely costly. For a standard surface code, magic-state distillation consumes 99 percent of the overall computation. Clearly, we need methods to improve or circumvent the need for magic-state distillation. Meanwhile, we can advance what we can do with noisy quantum computers using error mitigation. Instead of trying to design a quantum circuit to fix errors in computations in real-time (requiring extra qubits), error mitigation uses a classical computer to learn the contribution of noise from the outcome of noisy experiments and cancel it. You do not need additional qubits, but you pay the price in having to run more quantum circuits and introduce more classical processing.
For example, if you can characterize the noise in the quantum processor or learn it from a training set of noisy circuits that can be efficiently simulated in a classical computer, you can use that knowledge to approximate the output of the ideal quantum circuit. Think of that circuit as a sum of noisy circuits, each with a weight you calculate from the knowledge of noise. Or run the circuit multiple times, changing the value of the noise each time. You can then take the results, connect the dots, and extrapolate to the result you would expect if the system was error-free.
These techniques have limitations. They do not apply to all algorithms, and even when they apply, they get you only so far. But combining error mitigation with error correction produces a powerful union. Our theory team recently showed that this method could, by using error correction for Clifford gates and error mitigation for non-Clifford gates, allow us to simulate universal quantum circuits without needing magic state distillation. This outcome may also allow us to achieve an advantage over classical computers with smaller quantum computers. The team estimated that the particular combination of error mitigation and error correction lets you simulate circuits involving up to 40 times more non-Clifford gates than what a classical computer can handle.
To move forward and design more efficient ways of dealing with errors, there must be a tight feedback loop between hardware and theory. Theorists need to adapt quantum circuits and error correction codes to the engineering constraints of the machines. Engineers should design systems around the demands of error correction codes. The success of quantum computers hinges on navigating these theory and engineering trade-offs.
I’m proud to have played a role in shaping quantum computing from a field of lab-based demonstrations of one- and two-qubit devices to a field where anyone can access quantum systems with dozens of qubits via the cloud. But we have much to do. Reaping the benefits of quantum computing will require hardware that operates below the error threshold, error correction codes that can fix the remaining mishaps with as few additional qubits and gates as possible, and better ways to combine error correction and mitigation. We must press on because we haven’t finished writing the history of computation yet.








